
Atlas
The Celestial
Sphere
entities of the cosmological celestial mechanics first invented by Eudoxus,
adopted by Aristotle and developed by Ptolemy, Copernicus and others. In this
celestial model the stars and planets are carried around by being embedded in
rotating spheres made of an aetherial transparent fifth element (quintessence),
like jewels set in orbs.
In geocentric models the spheres were most commonly arranged outwards from
the center in this order: the sphere of the Moon, the sphere of Mercury, the
sphere of Venus, the sphere of the Sun, the sphere of Mars, the sphere of
Jupiter, the sphere of Saturn, the starry firmament, and sometimes one or two
additional spheres. The order of the lower planets was not universally agreed:
Plato and his followers ordered them Moon, Sun, Mercury, Venus, and then
followed the standard model for the upper spheres; there were other
disagreements about the relative place of the spheres of Mercury and Venus.
In his Metaphysics, Aristotle adopted a celestial physics of geo-concentric
rotating nested spheres first devised and developed by the astronomers Eudoxus
and Callippus. In the fully developed Aristotelian celestial physics, the
spherical Earth is at the center of the universe and the planets are attached to
anywhere from 47 to 55 concentric spheres that rotate around the Earth.
Aristotle considers that these spheres are made of an unchanging fifth element,
the aether, and each of these concentric spheres is moved by a god - an
unchanging divine mover. Aristotle says that to determine the exact number of
spheres and the number of divine movers, one should consult the astronomers.
The astronomer Ptolemy (fl. ca. 150 AD) defined a geometrical model of the
universe in his Almagest and extended it to a physical model of the cosmos in
his Planetary hypotheses. In doing so, he added mathematical detail and
predictive accuracy that had been lacking in earlier spherical models of the
cosmos. In Ptolemy's model, each planet is moved by two or more spheres (or
strictly speaking, by thick equatorial slices of spheres): one sphere is the
deferent, with a center offset somewhat from the Earth; the other sphere is an
epicycle embedded in the deferent, with the planet embedded in the spherical
epicycle. Through the use of the epicycle, eccentric, and equant, this model of
compound circular motions could account for all the irregularities of a planet's
apparent movements in the sky.
Christian and Muslim philosophers modified Ptolemy's system to include an
unmoved outermost region, which was the dwelling place of God and all the elect.
The outermost moving sphere, which moved with the daily motion affecting all
subordinate spheres, was moved by a fixed unmoved mover, the Prime Mover, who
was identified with God. Each of the lower spheres was moved by a subordinate
spiritual mover (a replacement for Aristotle's multiple divine movers), called
an intelligence.
Around the turn of the millennium, the Arabian astronomer and polymath Ibn
al-Haytham (Alhacen) presented a development of Ptolemy's geocentric epicyclic
models in terms of nested spheres. Despite the similarity of this concept to
that of Ptolemy's Planetary Hypotheses, al-Haytham's presentation differs in
sufficient detail that it has been argued that it reflects an independent
development of the concept. In chapters 15-16 of his Book of Optics, Ibn
al-Haytham also discovered that the celestial spheres do not consist of solid
matter.
Near the end of the twelfth century, the Spanish-Arabian Muslim astronomer
al-Bitruji (Alpetragius) sought to explain the complex motions of the planets
using purely concentric spheres, which moved with differing speeds from east to
west. This model was an attempt to restore the concentric spheres of Aristotle
without Ptolemy's epicycles and eccentrics, but it was much less accurate as a
predictive astronomical model.
In the thirteenth century, scholars in European universities dealt with the
implications of the rediscovered philosophy of Aristotle and astronomy of
Ptolemy. One issue that arose concerned the nature of the celestial spheres.
Through an extensive examination of a wide range of scholastic texts, Edward
Grant has demonstrated that scholastic philosophers generally considered the
celestial spheres to be solid in the sense of three-dimensional or continuous,
but most did not consider them solid in the sense of hard. The consensus was
that the celestial spheres were made of some kind of continuous fluid.
Early in the sixteenth century Nicolaus Copernicus drastically reformed the
model of astronomy by displacing the Earth from its central place in favour of
the sun, yet he called his great work De revolutionibus orbium coelestium (On
the Revolutions of the Celestial Spheres). Although Copernicus does not treat
the physical nature of the spheres in detail, his few allusions make it clear
that, like many of his predecessors, he accepted non-solid celestial spheres.
However, it seems a crucial physical reason for his heliocentrism in order to
save the celestial spheres may have been that he rejected the possibility of
interpenetrating spheres, but for some reason thought Martian parallax at
opposition is greater than solar parallax, whereby Mars must then be nearer the
Earth than the sun is, but also whereby the Martian and solar spheres must
intersect on all geocentric and geoheliocentric planetary models. They can only
be non-intersecting with Mars less than 1 AU away at opposition in the pure
heliocentric model. As Copernicus's pupil and herald Rheticus expressed this in
his 1540 Copernican Narratio Prima published 3 years before Copernicus's De
Revolutionibus, "Mars unquestionably shows a parallax sometimes greater than the
sun's, and therefore it seems impossible that the earth should occupy the centre
of the universe.". But this is only an impossibility for a spherist cosmology in
which different planetary spheres cannot intersect, but not for non-spherist
astronomy, as illustrated by the non-spherist Tychonic geocentric model, for
example, in which the Martian and solar orbits intersect (as also do the orbits
of Mercury and Venus with those of Mars and of Jupiter as drawn).
Tycho Brahe's observations that the comet of 1577 displayed less daily
parallax than the Moon implied it was superlunary and so, impossibly, must pass
through some planetary orbs in its transit. This led him to conclude that "the
structure of the heavens was very fluid and simple." Tycho opposed his view to
that of "very many modern philosophers" who divided the heavens into "various
orbs made of hard and impervious matter." Since Grant has been unable to
identify such a large number of believers in hard celestial spheres before
Copernicus, he concludes that the idea first became dominant sometime after the
publication of Copernicus's De revolutionibus in 1542 and either before, or
possibly somewhat after, Tycho Brahe's publication of his cometary observations
in 1588.
In Johannes Kepler's celestial physics the spheres were regarded as the
purely geometrical spatial regions containing each planetary orbit rather than
physical bodies as rotating orbs as in preceding Aristotelian celestial physics.
The eccentricity of each planet's elliptical orbit and its major and minor axes
thereby defined the lengths of the radii of the inner and outer limits of its
celestial sphere and thus its thickness. The intermediate causal role of these
annular geometrical spheres in Kepler's Platonist geometrical cosmology is to
determine the sizes and orderings of the five Platonic polyhedra within which
the spheres were supposedly spatially embedded.
Thus in Kepler's celestial mechanics the previous ultimate causal role of the
spheres became a non-ultimate intermediate role as the ultimate causal focus
shifted on the one hand to the Platonic regular polyhedra within which Kepler
held they were embedded and which thus ultimately defined the dimensions and
eccentricities of planetary orbits, and on the other hand to the rotating sun as
the central inner driver of planetary motion, itself rotated by its own motor
soul. However, an immobile stellar sphere was a lasting remnant of physical
celestial spheres in Kepler's cosmology.
But solid physical spheres still featured in both Galileo's and Newton's
early celestial mechanics, with Galileo initially considering the planets to be
rolling around the upper surfaces of fixed perfectly smooth spheres driven by
their own impetus and gravity, and with Newton calculating the centrifugal
pressure that would be exerted by the Moon on the lower concave surface of the
lunar orb in his 1660s analysis of lunar gravity. Thus for a long time Galileo
fiercely resisted the Tychonic theory that comets are superlunary because it
destroyed his initial spherist celestial mechanics by knocking away the
counter-gravitational supporting surfaces of the rolling planets, and he was
unable to explain circular orbits as closed curve projectiles driven by a
centrifugal impetus and centripetal gravity.
n Cicero's Dream of Scipio, the elder Scipio Africanus describes an ascent
through the celestial spheres, compared to which the Earth and the Roman Empire
dwindle into insignificance. A commentary on the Dream of Scipio by the late
Roman writer Macrobius, which included a discussion of the various schools of
thought on the order of the spheres, did much to spread the idea of the
celestial spheres through the Early Middle Ages.

Some late medieval figures inverted the model of the celestial spheres to
place God at the center and the Earth at the periphery. Near the beginning of
the fourteenth century Dante, in the Paradiso of his Divine Comedy, described
God as a light at the center of the cosmos. Here the poet ascends beyond
physical existence to the Empyrean Heaven, where he comes face to face with God
himself and is granted understanding of both divine and human nature.

Nicholas Oresme and his Spheres
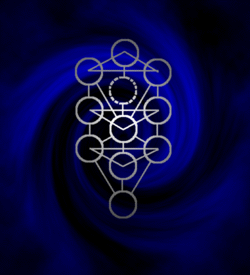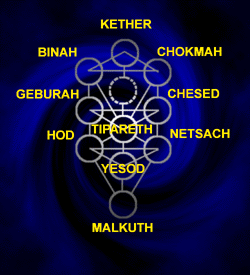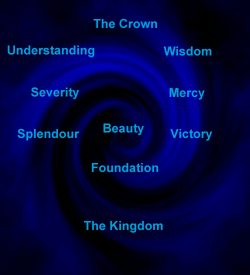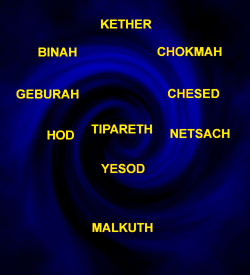
Reality is created by sound, tones, harmonics.
The spheres are the
harmonics on the Tree of Life.
They are the wheels of synchronicity that
create the illusion of linear time.

Universalis or Music of the Spheres is an ancient philosophical
concept that regards proportions in the movements of celestial bodies - the sun,
moon, and planets - as a form of musica - the medieval Latin name for
music. This music is not audible, but simply a mathematical concept.
The Greek philosopher Pythagoras is frequently credited with originating
the concept, which stemmed from his semi-mystical, semi-mathematical philosophy
and its associated system of numerology of Pythagoreanism. At the time, the sun,
moon, and planets were thought to revolve around Earth in their proper spheres.
The spheres were thought to be related by the whole-number ratios of pure
musical intervals, creating musical harmony.
There is a legend that Pythagoras could hear the 'music of the spheres'
enabling him to discover that consonant musical intervals can be expressed in
simple ratios of small integers. Pythagoras told the Egyptian priests that Thoth had spoken to him and given him the ability to hear
the harmony of the spheres. The tones correlated with the great celestial
movements of the day. Pythagoras knew that only Egyptians of the 'right'
bloodline, passing successful initiations, could enter the temples and learn the
mysteries set in place by the gods at the beginning of time. To learn more he
had to win their confidence and needed to appear as a royal soul, begat of the
gods and above the sins of man. Pythagoras' concepts were transferred by Plato and others - into models about the structure of the
universe.

Johannes Kepler used the
concept of the music of the spheres in his Harmonice Mundi Harmony of
the Worlds in 1619.
According to Max Heindel's Rosicrucian writings, the heavenly "music of the
spheres" is heard in the Region of Concrete Thought, the lower region of
the World of Thought,
which is an ocean of harmony. It is also referred in Esoteric Christianity
that this is the place where it occurs the state of consciousness called the
"Second heaven."
There are three branches of the Medieval concept of musica:
- musica universalis (sometimes referred to as musica mundana)
- musica humana (the internal music of the human body)
- musica instrumentalis (sounds made by singers and instrumentalists)
Harmony of the
Spheres

Sacred
Geometry

No comments:
Post a Comment